Areas, A Package that Solves Certain Practical Problems in Topology
David J. Kennison
NCAR, P.O. Box 3000, Boulder, Colorado 80307-3000
email: kennison@ucar.edu
Table of Contents
This document is the reference manual for an NCAR Graphics package called
AREAS, which was written in 1985 or 1986 as a first step in writing a
solid-fill global mapping package (EZMAPA) and a new contouring package
(CONPACK). In the years that have passed since AREAS was first written, it
has been significantly improved. Various errors have been corrected. It now
automatically uses single-precision, double-precision, or multiple-precision
arithmetic, depending on the characteristics of the machine on which it is
running. Some useful debugging tools have been added. Edges being put into
an area map are now clipped at the edges of the plotter frame.
At least three major problems led to the writing of AREAS:
- NCAR Graphics contains a database of global geographic outlines and a
package of routines called EZMAP that allow one to draw maps of the
globe in any of ten different projections. Originally, EZMAP could
only produce line drawings; it was desired to be able to fill the
various areas defined by the geographic outlines, either with different
colors or with different patterns.
- Replacement of the contouring routines CONREC and CONRAN was being
contemplated. It was considered important to be able to color-fill
and/or pattern-fill contour bands, to inhibit the drawing of contour
lines through contour labels, and to limit the drawing of contour lines
to certain areas of the plane (those areas over land or over ocean on a
given projection of the globe, for example). Moreover, it was considered
important that, given a set of geographic outlines on a given global map
and a set of contour lines on the same map, one should be able to recover
the definition of each of the various areas created by those lines, each
such area being accompanied by information allowing one to determine what
geographic entity and what contour band that area lay within.
- A number of users had expressed the desire to construct a global grid
of data, where each datum is a 0 if the grid point is over water or a
1 if the grid point is over land (or, perhaps, a 0 to indicate water
and a non-zero integer to identify a particular land mass).
The reader might well pause here and consider what sort of tool he/she would
create to solve all of these problems. AREAS is one answer.
The graphical output from the AREAS examples "arex01",
"arex02", and "arex03" will be
very helpful to have on hand while reading this document.
The package AREAS allows one to create, modify, and use, in various ways,
structures called "area maps". (See the graphical output from example
"arex01" for depictions of an area map in various
states.)
An "area map" is basically a set of straight-line segments in the plane;
each of these segments is called an "edge segment". Each "edge segment"
connects two distinct points in the plane; associated with it in the area
map are three integers: a "group identifier", a "left area identifier",
and a "right area identifier".
By convention, the group identifier associated with an edge segment is
always a positive, non-zero integer - preferably a value between 1 and 16,
inclusive. The set of all edge segments in an area map that have group
identifier G is referred to as "edge group G";. There are as many edge
groups in an area map as there are distinct group identifiers associated
with the edge segments in the area map.
The edge segments in a given edge group are normally all related to each
other in some way. For example, the edge segments in one edge group might
all be boundary lines from the geographic outline database, mapped into a
plane; the edge segments in another edge group might be contour lines for
some physical quantity on the surface of the globe, mapped into the same
plane.
An "area" defined by a set E of edge segments in the plane is a set S of
points in the plane such that 1) if the points P and Q are both members
of S, there exists a continuous curve, in the plane, that connects P and
Q and that nowhere crosses any of the edge segments in E, and 2) if the
point P is a member of S and there exists a continuous curve, in the plane,
that connects the point P to some other point Q without crossing any of the
edge segments in E, then Q is also a member of S. (Note: Proving that this
definition of "area" is meaningful requires some rather high-powered
mathematical machinery. Luckily, none of that machinery is needed to use
AREAS - or to write the code, for that matter.)
A given set of edge segments defines at least one area; it may define only
one area (the entire real plane), but useful sets of edge segments will
usually define more than one (and, probably, many) areas. For example, if
the edge segments in the set all come from a database of geographic
outlines, then the areas defined may be islands, continents, lakes,
countries, etc. One of the areas defined will always be unbounded and the
rest will be bounded.
The set of areas defined by all edge segments in an area map having group
identifier G (that is to say, by edge group G) will be referred to as "area
group G". An area map defines as many area groups as there are edge groups
in the area map.
Observe that, if A is the set of areas defined by all the edge segments in
an area map and G is a particular group identifier, then any member of A is
wholly contained in some member of area group G. For example, if there are
two edge groups, one of which defines geographic entities and the other of
which defines contour bands, then each of the areas defined by the union of
all the edge segments is contained in precisely one geographic entity and
in precisely one contour band.
The area identifiers associated with the edge segments in edge group G are
ultimately used to assign an area identifier to each of the areas in area
group G. The idea here is that, if one has a way of generating boundary
lines, one generally knows what lies on either side of each boundary line.
For example, the geographic outline database has, associated with each
piece of outline, a couple of integers identifying the geographic entities
that are separated by that piece of outline. Similarly, when one traces
contour lines, one can assign identifying integers to all of the contour
bands and one knows what two contour bands each contour line separates.
Normally, one uses positive, non-zero area identifiers for areas of
interest.
Area identifiers that are negative are all treated as being equal to -1
and have a special use: they indicate that the area is somehow outside the
"perimeter" of the area group, where "perimeter" might be loosely defined
as the boundary of that part of the plane that is of interest relative to
the area group. For example, each edge group put in an area map is
automatically augmented by four edge segments defining a rectangular
perimeter at the boundary of the plotter frame; the area identifier
for the area outside this rectangle is specified as a -1, indicating
that what is outside that rectangle is, in some manner, of no interest.
Area identifiers that are zero have a different special use. They are used
to indicate that one does not know what area identifier to use and that one
must depend on the required information to be supplied with some other edge
segment in the area map. For example, area identifiers for areas toward the
inside of the automatically-supplied rectangular perimeter are specified as
zeroes.
The boundary of a particular area defined by a set of edge segments is a
subset of that set of edge segments. Each of those edge segments is oriented
so that the area is either to its left or to its right (where "left" and
"right" are defined from the viewpoint of an observer at the first point of
the edge segment, looking toward the second point of the edge segment, and
the ordering of the points is determined by the order in which they are
seen by AREAS); thus, we can decide whether its left area identifier or
its right area identifier ought to be the area identifier for the area.
By examining all of the edge segments on the boundary of an area, we get a
collection of possible area identifiers for it. If all of the values are
the same, there's no problem; that's the value we use.
For various reasons, the set of possible area identifiers for a given area
(relative to a particular group) may be self-contradictory. In that case,
some algorithm must be used to choose an area identifier for the area:
- The algorithm used by default (when the element of the internal
parameter array 'RC' associated with the edge group has the value 0)
is as follows: If any of the possible area identifiers is negative,
use a -1. Otherwise, if none of the possible values is non-zero, use
a zero. Otherwise, from among the non-zero possibilities, choose the
one that was most recently seen by AREAS.
- If the value of the 'RC' element is set to 1, then the set of possible
area identifiers is examined: Zeroes are ignored, negatives are treated
as -1's, and the value that occurs most frequently in the resulting set
is used.
- Using an 'RC' element = 2 is just like using a 1 except that zeroes
are not ignored: the final value is simply that one which occurs most
frequently in the set of possibilities (all negatives being treated
as equal to -1).
- Using an 'RC' element = -1 or -2 is just like using a 1 or a 2,
respectively, except that, if there are any negative values in the
set of possibilities, then a -1 is used for the area.
The graphical output from the example "arex03"
illustrates the use of each of these values.
Once an area map has been created, one might want to do one or more of
the following things with it:
- Given a point P, in the plane, one might wish to know, for each group
identifier G, what area identifier has been assigned to the area in
area group G that contains the point P.
- Given a "polyline" in the plane (a continuous curve composed of
straight-line segments), one might wish to obtain a set of pieces
of that polyline such that each piece lies in one of the areas
created by the set of all edge segments in the area map. For each
such piece, one might also wish to know, for each group identifier
G, what area identifier has been assigned to the area in area group
G that contains that piece.
- One might wish to obtain all of the areas created by the set of all
edge segments in the area map. For each such area A, one might then
wish to know, for each group identifier G, what area identifier has
been assigned to the area in area group G that contains A.
Each of these things can be done with the package AREAS.
The routine ARINAM ("AReas, Initialize Area Map") is used to initialize an
area map. One executes the FORTRAN statement
CALL ARINAM (IAM,LAM)
where IAM is an integer array (sometimes referred to as an "area map array"),
dimensioned at least LAM, in which the representation of an area map is to
be constructed. Upon return, IAM will contain the representation of a null
area map (one containing no edge segments at all).
How big does an area map array have to be? A rough answer is "pretty big".
To come up with a more precise answer, one needs information from the next
three sections: Adding Segments to an
Area Map, Preprocessing an Area Map,
and Using an Area Map; the detailed
description of the structure of area map arrays that is given in the
section called Details may also be of use.
One way to proceed is to declare a really big area map array, put some edge
segments in it, and use it for something; after each call to an AREAS
routine, one can examine the area map array to see how much of the
available space has actually been used. This can be done because, at any
given time after an area map array has been initialized, only elements 1
through IAM(5) and elements IAM(6) through LAM of IAM are actually being
used, so the expression
LAM-(IAM(6)-IAM(5)-1)
says how much space in IAM is really being used. Note that the routine
ARPRAM expands the amount of space used by quite a bit and that both of
the routines ARPRAM and ARSCAM use a little more space while they are
executing than is used when they finish executing.
Additional useful information will be found in the section called
Moving an Area Map, which describes how
to move an area map from one integer array to another, and in the section
called Error Handling, which describes how
to get control back when an error has occurred (in particular, when an
area map has become too large for the area map array). See also the
example "arex02", which shows how to construct
a scheme for dealing with area map array overflows.
The routine AREDAM ("AReas, EDge to Area Map") is used to add edge segments
to an area map. It is called by executing the FORTRAN statement
CALL AREDAM (IAM,XCA,YCA,LCA,IGI,IDL,IDR)
where IAM is the integer area-map array to which edge segments are to be
added, XCA and YCA are real arrays holding the X and Y coordinates (in the
"user" coordinate system) of points defining an "edge", LCA is the number
of coordinates in the arrays XCA and YCA, IGI is a group identifier, IDL
is a left area identifier, and IDR is a right area identifier.
Let the points defined by the arrays XCA and YCA be called P1, P2, P3, ...,
Pn, where "n" is the value of "LCA". AREDAM adds to the area map each of
the n-1 edge segments joining P1 to P2, P2 to P3, P3 to P4, ..., and Pn-1
to Pn; "n" must be greater than or equal to 2, and, for all i from 2 to n,
Pi must be distinct from Pi-1. The group identifier IGI and the area
identifiers IDL and IDR are used for each of the edge segments placed in
the area map.
The X and Y coordinates are specified in the "user" coordinate system;
AREDAM maps them to the fractional system, as directed by the latest call
to the SPPS routine SET (or by the equivalent GKS calls), and then to an
integer coordinate system in which the lower left corner of the plotter
frame has coordinates (0,0) and the upper right corner of the plotter
frame has coordinates ('LC','LC'). ('LC' is an internal parameter of
AREAS with a default value of 1,000,000.) The resulting integer values
are stored in the area map array.
Note that, in between one set of calls to AREDAM and another, one can put
a call to SET that changes the mapping from the "user" system to the
"fractional" system. One set of edge segments might be defined using the
SET call done by the package EZMAP and the next set of edge segments might
be defined using a SET call that allows the input values in XCA and YCA to
be given in the fractional coordinate system. Once the X and Y coordinates
are stored in the area map array, though, they have fixed positions
relative to the plotter frame that are unaffected by subsequent calls to
SET.
Prior to version 4.1 of NCAR Graphics, it was the case that, if the linear
transformation from a user coordinate to an integer coordinate produced a
value less than zero, a zero was substituted. Similarly, if the linear
transformation from a user coordinate to an integer coordinate produced
a value greater than 'LC', the value 'LC' was substituted. This had two
implications:
- One could not create a meaningful area map that included anything
outside the plotter frame.
- If an edge segment was defined in such a way that one of its endpoints
was inside the plotter frame and the other endpoint was outside the
plotter frame, what went into the area map was not the portion of the
edge segment that lay within the plotter frame, neatly clipped by the
edges of it, but whatever edge segment resulted from the substitution
process.
As of version 4.1 of NCAR Graphics, the code of AREDAM has been changed
to properly clip edge segments at the boundary of the plotter frame; it
is still not possible to create an area map representing something
outside the plotter frame.
The first time that AREDAM sees a particular group identifier G, it adds
four extra edge segments to the area map; these edge segments define the
boundary of the plotter frame - the square bounded by the lines X = 0, X
= 'LC', Y = 0, and Y = 'LC' (in the coordinate system used internally by
AREAS); the group identifier for each of these edge segments is set to G
and their area identifiers are set so as to say that the areas inside the
square and outside the square have area identifiers 0 and -1, respectively.
These edge segments form a default "perimeter" for the edge group G.
Each call to AREDAM increases the amount of space used in the area map
array by 10*LCA (for storage of endpoints), plus 1 if the group identifier
used is a new one, plus 1 if the left area identifier is a new one, plus
1 if the right area identifier is a new one.
The routine ARPRAM ("AReas, PReprocess Area Map") is called to "preprocess"
an area map. It may be called by the user, if he/she wishes to do so; the
only advantage of this is that the user may then specify the use of certain
time-saving shortcuts (if they are known to be "safe" because of the nature
of the area map that has been defined).
There is a flag in the area map array that, if set, says that the area map
has been "preprocessed"; a user call to ARPRAM sets this flag, so that other
AREAS routines that require preprocessing to have been done will know whether
or not it needs to be done before proceeding. Any call to AREDAM that adds
more edge segments to the area map clears this flag again.
The FORTRAN statement used to call ARPRAM is as follows:
CALL ARPRAM (IAM,IF1,IF2,IF3)
where IAM is the integer area map array and IF1, IF2, and IF3 are "shortcut"
flags. Each shortcut flag is an integer, set to zero if the shortcut is not
to be taken or to one if the shortcut is to be taken. Anytime that AREAS
itself calls AREDAM, it sets all of the shortcut flags to zero.
If the taking of a particular shortcut is requested and ARPRAM decides that
taking that shortcut led to a problem, it will attempt to fix the problem
by redoing the bypassed step with the shortcut turned off.
ARPRAM transforms the area map by performing the seven steps detailed below.
The example called "arex01" produces a set of plots
showing what ARPRAM does; those plots will help to clarify and explain the
following text.
Any edge segment whose projection on the X axis is longer than twice the
average is replaced by two or more edge segments whose projections on the
X axis are about as long as the average. An edge segment joining a point
P to a point Q is replaced by the edge segments joining P to I1, I1 to I2,
I2 to I3, ... In-1 to In, and In to Q, where I1, I2, ... In are "n"
equally-spaced points interpolated along the line segment from P to Q.
This step is done for all edge segments in the area map, without regard
to the group identifiers of the edge segments. It is done in order to
speed up some of the algorithms used in other steps (that otherwise tend
to run in geologic time).
If an edge segment in the area map is crossed by another edge segment in
the area map at a point distinct from either of its end points, then it
is replaced by two edge segments; the edge segment joining a point P to
a point Q is replaced by the edge segments joining P to I and I to Q,
where I is the point of intersection with some other edge segment in the
area map.
This step is done for all edge segments in the area map, without regard
to the group identifiers of the edge segments. It ensures that, if we
start at a particular point P in the area map and begin following edge
segments from point to point to form a continuous curve in the plane and
if, at each point, we always choose either the leftmost adjoining edge
segment or the rightmost adjoining edge segment from a particular set of
edge segments, then the curve will eventually close on itself (by returning
to P) and will form the outer boundary of one of the areas defined by that
set of edge segments (or a "hole" in one of those areas - see
step 5, below).
If IF1 is set non-zero, a pair of edge segments is examined to see if they
intersect only if one of the pair has a left or right area identifier that
is zero or negative. This would be appropriate, for example, for contour
lines,which are known not to intersect each other, but only to intersect
the perimeter.
The area map is searched for coincident edge segments (a pair of edge
segments, each of which has endpoints P and Q). Whenever two such
coincident edge segments are found, what happens depends on whether or
not they have the same group identifier. If not, the representation of
one edge segment in the pair is modified in such a way that it will appear
to be present when looking for areas defined by edge segments having the
same group identifier, but absent when looking for areas defined by all
the edge segments, ignoring the group identifier. If, on the other hand,
both members of a coincident pair belong to the same group, one of the
edges is removed from the area map and the left and right area identifiers
of the remaining one are adjusted to incorporate reconciled information
from the pair. The "reconciliation" is done in a somewhat heuristic fashion
that seems to work fairly well in real cases of interest: if both members
of the pair imply that a negative value should be used, the result is "-1";
if both imply that a particular value greater than zero should be used, the
result is that value; in all other cases, the result is zero. (Note that,
in version 3.2, a zero paired with a value greater than zero would give you
the latter value; now, it gives you a zero.)
This step ensures that if, while following the curve forming the outer
boundary of an area defined by the area map (or a "hole" in such an area),
as described in step 2, above, we mark each of the edge segments used in
such a way as to say that the area to its left (or right, whichever is
appropriate) has been "seen", then, when we search the area map for an
unmarked edge segment (so as to start tracing the curve forming another
such boundary), we will not find an edge segment that leads to our trying
to retrace the first boundary.
Each edge group in the area map is searched for edge segments that do not
contribute to forming any areas relative to that edge group; all such edge
segments are removed from the area map. More precisely: if an edge segment
having group identifier G has endpoints P and Q, but there is no other edge
segment in the area map having group identifier G and having P as an
endpoint (or, alternatively, there is no other edge segment in the area
map having group identifier G and having Q as an endpoint), then the edge
segment with endpoints P and Q is removed from the area map.
Since the removal of a particular edge segment may make another edge
segment, previously considered and rejected, into a candidate for removal,
step 3 is repeated (in effect), until no further candidates for removal are
found.
This step simply removes from the area map edge segments that cannot
possibly affect anything.
If IF2 is non-zero, step 4 is skipped. This is appropriate for contour
lines, which are known not to have any such "dangling" edge segments, but
it is not appropriate for EZMAP boundary lines. (The EZMAP dataset contains,
for example, islands that are formed from simple unclosed curves.)
Each edge group in the area map is searched for areas with "holes"; each
time a "hole" is found, a temporary edge segment is added to the area map,
effectively removing the "hole" from the area map. Roughly speaking, an
area with a "hole" is like a doughnut (or, better, a thin slice of Swiss
cheese). The boundary of such an area is not a simple closed curve, but a
collection of closed curves, none of which crosses or touches any of the
others. One of the closed curves defines the outer boundary of the area.
The others are completely enclosed within this outer boundary and are the
"holes".
Holes are detected in the following manner: As we use the process described
in step 2 to follow the boundary of an area, we can keep track of the
cumulative angular change in direction along the boundary that is being
generated. When we arrive back at our starting point, the total angular
change in direction will be either -360 degrees or +360 degrees. If, at
each step in tracing the boundary, we choose the leftmost available edge
segment and the total angular change turns out to be +360 degrees or if,
at each step in tracing the boundary, we choose the rightmost available
edge segment and the total angular change turns out to be -360 degrees,
then what we have just traced is the outer boundary of an area; otherwise,
it is the boundary of a hole in an area.
Once a hole is detected, a connecting edge segment is created by joining
the point P having the largest Y coordinate on the boundary of the hole
to a point Q on the first edge segment in the current edge group that is
encountered as one draws a line from the point P in the positive Y
direction; usually, the point Q will have to be interpolated in the area
map and the edge segment encountered replaced by two new edge segments
emanating from Q. All of this is done in such a way that, in step 7, these
connecting edge segments can be removed from the area map again.
This step is done in order that all the area-identifier information for
an area with a hole should be taken into account in selecting an area
identifier for that area.
If IF3 is set non-zero, this step is skipped. This is appropriate when
it is known that the area-identifier information is complete and that the
consideration of holes cannot change the area identifiers chosen for an
area that contains a hole. This should be appropriate for contour lines
and for the EZMAP dataset.
Each edge group in the area map is examined separately; for each of the
edge groups, each area defined by that edge group is examined. For each
edge segment that forms a part of the boundary of the area, we determine
which of the area identifiers (either the left one or the right one)
applies to the area we are examining. (If the edge segment has endpoints
P and Q and the point P preceded the point Q in the edge defined by the
call to AREDAM that resulted in the edge segment's being put in the area
map, then "left" and "right" are defined from the viewpoint of an observer
at the point P, looking toward the point Q.) The area identifiers for a
particular area may contradict one another; contradictions are resolved,
a single identifier for the area is chosen, and the resulting value
replaces all of the area identifiers that were examined.
This step ensures that all the area identifiers in an area map are
consistent with each other; in turn, this ensures that, to find the area
identifier for a particular area, all we need to find is a single edge
segment that is known to be part of the boundary of the area.
The connecting lines that were inserted, in step 5, to remove the holes
from areas in the area map, are taken out.
This step simply removes temporary structures that are not needed any
more.
Step 1 can significantly increase the amount of space used in an area
map.
Step 2 can slightly increase the amount of space used in an area map.
Step 3 does not change the amount of space used in the area map; the space
occupied by removed edge segments is not reused.
Step 4 does not change the amount of space used in the area map; the space
occupied by removed edge segments is not reused.
Step 5 can increase slightly the amount of space used in the area map.
Step 6 does not change the amount of space used in the area map.
Step 7 decreases the amount of space used in the area map by the amount
that step 5 increased it.
Once an area map array has been initialized and edge segments have been
added to it, any of three routines may be called to use the area map in
that area map array: ARGTAI is used to get the area identifiers for the
area containing a specified point; ARDRLN is used to break a specified
polyline into pieces, each of which lies in only one of the areas defined
by the area map; and ARSCAM is used to obtain, one by one, the areas defined
by the area map. Another routine, ARDBPA, may be called to produce debug
plots of the various edge groups in the area map.
The routine ARGTAI ("AReas, GeT Area Identifiers") may be used to get the
area identifiers associated with a given point. It is called using the
following FORTRAN statement:
CALL ARGTAI (IAM,XCD,YCD,IAI,IAG,MAI,NAI,ICF)
IAM is the area-map array. XCD and YCD are the real X and Y coordinates,
in the current user coordinate system, of a point at which information is
desired, and IAI and IAG are integer arrays, each dimensioned MAI, in which
the information is to be returned.
Upon return from the call to ARGTAI, NAI will have been set to the number
of groups of areas in the area map and, for each I from 1 to NAI, IAI(I)
will be an area identifier and IAG(I) the associated group identifier.
ICF is a input flag, set non-zero by the user to indicate that the
definition of the user coordinate system has been changed since the last
call to ARGTAI, in which case a call to GETSET must be executed by ARGTAI;
if the flag is zero, it will be assumed that the information retrieved
previously is still correct and that the call to GETSET may be skipped.
If a single point is being inquired about, ICF should just be set non-zero.
If a lot of points are being inquired about, and the call to SET will not
be redone in between one call to ARGTAI and the next, then ICF should be
set non-zero for the first call and zero for all the rest, thus avoiding
a lot of calls by ARGTAI to GETSET.
The routine ARDRLN ("AReas, DRaw LiNe"), given a polyline and an area map,
breaks the polyline into pieces in such a way that each piece lies within
one of the areas defined by all the edge segments in the area map. For
each such piece of the polyline, a user-specified routine is called. That
routine may choose to draw (or not to draw) each piece. This technique may
be used, for example, to limit the drawing of lines of latitude and
longitude to areas over the ocean. In the package CONPACK, it is used
to keep contour lines from passing through contour labels. This process
is sometimes referred to as "masking" the polyline against an area map.
ARDRLN is called using the following FORTRAN statement:
CALL ARDRLN (IAM,XCD,YCD,NCD,XCS,YCS,MCS,IAI,IAG,MAI,LPR)
IAM is the integer area map array. XCD and YCD are real arrays of X and Y
coordinates, in the current user coordinate system, defining the polyline.
NCD is the number of coordinates in XCD and YCD. XCS and YCS are real
coordinate arrays for ARDRLN to use in calls to the user-supplied
line-processing routine; each is dimensioned MCS. Similarly, IAI and IAG
are integer arrays, each dimensioned MAI, in which the area identifiers
and group identifiers are to be passed to the user-supplied line-processing
routine. LPR is the name of the user-supplied line-processing routine; this
name must appear in an EXTERNAL statement in the routine that calls ARDRLN.
The routine LPR must be supplied by the user and must have the
following structure:
SUBROUTINE LPR (XCS,YCS,NCS,IAI,IAG,NAI)
DIMENSION XCS(*),YCS(*),IAI(*),IAG(*)
... (code to process the polyline defined by the arguments) ...
RETURN
END
The arrays XCS and YCS will contain NCS fractional coordinates (in the
range from 0. to 1., inclusive) of the points defining a piece of the
original polyline. For each I from 1 to NAI, IAI(I) will be the area
identifier selected for the area with respect to the group IAG(I).
Before executing the first call to LPR, the routine ARDRLN executes
the following two statements:
CALL GETSET (VPL,VPR,VPB,VPT,WDL,WDR,WDB,WDT,LLG)
CALL SET (VPL,VPR,VPB,VPT,VPL,VPR,VPB,VPT, 1)
This ensures that, if the normalized device coordinates in XCS and
YCS are used by APR in calls to such routines as GPL and CURVE, the
results will be correct. Of course, the routine LPR may do its own
SET call to achieve some other effect. Before finally returning control
to the caller, ARDRLN recalls SET to restore the original mapping.
The routine ARSCAM ("AReas, SCan Area Map") is called by executing the
following FORTRAN statement:
CALL ARSCAM (IAM,XCS,YCS,MCS,IAI,IAG,MAI,APR)
IAM is the integer area map array. XCS and YCS are real work arrays of
size MCS, to be used by ARSCAM in calls to a user-supplied area-processing
routine. IAI and IAG are integer work arrays of size MAI, also to be used
by ARSCAM in calls to that routine. APR is the name of the area-processing
routine; this name must appear in an EXTERNAL statement in the routine that
calls ARSCAM.
ARSCAM scans the area map from left to right, extracting, one by one, the
areas defined by all the edge segments in the area map and, for each one,
calling the routine APR to process the area.
The routine APR must be supplied by the user and must have the following
structure:
SUBROUTINE APR (XCS,YCS,NCS,IAI,IAG,NAI)
DIMENSION XCS(*),YCS(*),IAI(*),IAG(*)
... (code to process the area defined by the arguments) ...
RETURN
END
The arrays XCS and YCS will contain NCS fractional coordinates (in the
range from 0. to 1., inclusive) of the points defining the boundary of
the area. The last point will be a duplicate of the first. Holes in an
area will be traced in such a way as to maximize the probability of
hardware fill working properly (at least on the devices that I know
about), using vertical lines to get to and from the holes and tracing
them in the proper direction. For each I from 1 to NAI, IAI(I) will be
the area identifier for the area with respect to the group IAG(I).
Before executing the first call to APR, the routine ARSCAM executes the
following two statements:
CALL GETSET (VPL,VPR,VPB,VPT,WDL,WDR,WDB,WDT,LLG)
CALL SET (VPL,VPR,VPB,VPT,VPL,VPR,VPB,VPT, 1)
This ensures that, if the normalized device coordinates in XCS and YCS
are used by APR in calls to such routines as GFA and FILL, the results
will be correct. Of course, the routine APR may do its own SET call to
achieve some other effect. Before returning control to the caller, ARSCAM
recalls SET to restore the original mapping.
In the routine APR, the statement
CALL ARGETI ('DI - DIRECTION',IDI)
sets the value of the integer variable IDI to 1 if the edge of the area
is specified in counterclockwise order (with the interior to the left) or
to 2 if the edge of the area is specified in clockwise order (with the
interior to the right). This information may be needed for some
purposes.
The routine ARDBPA (for "AReas, DeBug, Plot Area map") is called by
executing the FORTRAN statement
CALL ARDBPA (IAM,IGI,LAB)
IAM is an area map array that has at least been initialized (by calling
ARINAM). IGI is an integer which, if greater than zero, specifies a
particular group identifier. LAB is a character string to be used as a
label.
This call produces a plot showing all the edge segments in the area map
array IAM that belong to group IGI; if IGI is less than or equal to zero,
all edge segments are shown. The label specified by LAB is written at the
top of the plot.
The internal parameter 'DB' may be set to request that the routine ARPRAM
call ARDBPA at each of a number of breakpoints of interest.
Each edge segment selected for display is shown as an arrow; in regions
where there are lots of very short edge segments, some or most of the
arrowheads are omitted. The size of the arrowheads used is specified by
the values of two internal parameters of AREAS called 'AL' and 'AW';
these parameters may be given values which will cause the arrowheads to
be omitted.
The left and right area identifiers that are associated with an edge
segment are written just to the left and just to the right, respectively,
of the midpoint of the arrow representing that edge segment (where "left"
and "right" are defined from the viewpoint of an observer at the tail of
the arrow, looking toward the head of the arrow). If IGI is less than or
equal to zero, the group identifier of the edge segment is written at the
midpoint of the arrow. The size of the characters used to write the
identifiers and the distances of the area identifiers from the arrow are
specified by the values of two internal parameters of AREAS called 'IS'
and 'ID'; by default, they are written using very small characters - so
small that one cannot read them without using something like the "zoom"
capability of "idt". This is by design; the idea is that one can look at
the global picture and then, if something of interest is seen, zoom in
to see what is happening locally, at which point the area identifiers
are actually of interest.
ARDBPA redefines and uses color indices 'DC'+1 through 'DC'+5, where 'DC'
is one of the internal parameters of AREAS and has the default value 100.
Four of the colors used for the edge segments depend on the area
identifiers, as follows:
| Color | Left area identifier | Right area identifier |
| magenta | less than or equal to zero | less than or equal to zero |
| yellow | less than or equal to zero | greater than zero |
| cyan | greater than zero | less than or equal to zero |
| white | greater than zero | greater than zero |
The fifth color, gray, is used for any edge segment that is coincident
with an edge segment in one of the other edge groups and has not been
chosen to be the one that appears to be there where scanning for areas
relative to the set of all edge segments in the area map. This
distinction is probably not of great interest to the average user, and
is basically provided for the author's use.
After drawing the requested plot, ARDBPA calls the SPPS routine FRAME
to advance the plotter frame.
Moving an area map is useful for two purposes: 1) to pack an existing area
map into the smallest possible space; and 2) during error recovery, to move
an area map from a too-small array to a bigger array. In order for this to
be useful, some sort of memory-management scheme must be employed; this can
be done most effectively in C or in Fortran 90, rather than in Fortran 77.
The example named "arex02" may be helpful; it shows
how to recover (albeit somewhat clumsily) from area map array overflows in
a Fortran 77 context.
Moving an area map from one integer array to another is not totally
straightforward, because two portions of the array are used, a portion at
the beginning and a portion at the end, and because some elements in the
first portion are pointers to elements in the second portion. Both portions
have to be moved, and the values of the pointers must be adjusted to point
to the correct elements in the new array.
The routine ARMVAM ("AReas, MoVe Area Map") is called to move an area map
from one integer array to another. It is called using the following Fortran
statement:
CALL ARMVAM (IAM,IAN,LAN)
IAM is the integer array containing the area map to be moved, and IAN is the
integer array to which it is to be moved. LAN is an integer expression, the
value of which is the length of the array IAN.
The argument IAM must have previously appeared in a call to ARINAM (to
initialize the area map). More than likely, it will also have appeared in
one or more calls to AREDAM (to add edges to the area map). The length of
IAM does not have to be provided as an argument in a call to ARMVAM, because
it is available as part of the contents of IAM.
Upon return from a call to ARMVAM, the contents of the array IAM will be
unchanged if and only if the arrays IAM and IAN do not overlap in memory.
If IAM and IAN do overlap, they must start at the same location in memory.
The move will be done in such a way as to avoid problems that could arise
because of the overlap: If the move is from a smaller array to a bigger
one, the move index steps backwards in memory, but if the move is from a
bigger array to a smaller one, the move index steps forwards in memory.
This has been done so that, during recovery from area-map-array-overflow
conditions, one need not provide room for both the original array and a
new array at the same time: if the original array can be lengthened in
place, then the area map can simply be expanded from the old space into
the new space.
AREAS has the following internal parameters (each with a two-character
mnemonic name):
- 'AL' ("Arrowhead Length") is of type REAL. It specifies the length of
the arrowheads to be used on debug plots.
- 'AT' ("Arithmetic Type") is of type INTEGER. It specifies the type of
arithmetic to be used by AREAS.
- 'AW' ("Arrowhead Width") is of type REAL. It specifies the width
(actually, the half-width) of the arrowheads to be used on debug plots.
- 'DB' ("Debug Plots") is of type INTEGER. If non-zero, it specifies the
identifier of the group of edge segments to be depicted on debug plots
done by ARPRAM. Use a "-1" to see all groups of edge segments.
- 'DC' ("Debug Colors") is of type INTEGER. If debug plots are done, color
indices 'DC'+1 through 'DC'+5 are defined for use on the plots.
- 'ID' ("Identifier Distance") is of type REAL. It specifies, on debug
plots, the distance from the arrow representing an edge segment to each
of the area identifiers for the segment.
- 'IS' ("Identifier Size") is of type REAL. It specifies the size of the
characters to be used to write the area identifiers on debug plots.
- 'LC' ("Largest Coordinate") is of type INTEGER. It specifies the
resolution of the grid used by AREAS to represent the plotter frame.
- 'RC' ("Resolving-Contradictions flag array") refers to a 16-element
array, indexed by group identifier, of type INTEGER. Values in it
determine in what manner contradictions in the area-identifier
information for an area are to be resolved.
Another internal parameter, whose value cannot be set, has already been
mentioned above, in the description of the routine ARSCAM; its value is for
retrieval only:
- 'DI' ("DIrection") is of type INTEGER. It has a value indicating in
which direction (counterclockwise or clockwise) a polygon delivered to
the routine APR by ARSCAM was traced.
All of these parameters are described in more detail in following sections.
Some of the internal parameters have integer values and some have real
values. To reset the value of an internal parameter, use a call like
CALL ARSETI ('AT - ARITHMETIC TYPE',DESIRED_INTEGER_VALUE_OF_'AT')
or
CALL ARSETR (`AW - ARROWHEAD WIDTH',DESIRED_REAL_VALUE_OF_'AW')
The first argument is a character string giving the name of the parameter
whose value is to be set. Usually, only the first two characters of this
character string are examined; other characters may be used to make the
code easier to read.
When the parameter array 'RC' is being accessed, the parameter name may
appear in the form "RC(n)", where "n" is an integer between 1 and 16,
inclusive, to select a particular element of the array; additional
characters following the closing parenthesis are ignored.
The second argument is an integer expression specifying the value that
is to be given to the parameter. The type of this argument must be INTEGER
in a call to ARSETI and REAL in a call to ARSETR. If the type of the
argument does not match the type of the internal parameter, the appropriate
conversion (using the intrinsic function INT or REAL) will be done for
you.
To retrieve the value of an internal parameter, use a call like
CALL ARGETI ('AT - ARITHMETIC TYPE',IAT)
or
CALL ARGETR ('AW - ARROWHEAD WIDTH',RAW)
The first argument is a character string giving the name of the parameter
whose value is to be retrieved. Usually, only the first two characters of
this character string are examined; other characters may be used to make
the code easier to read.
When the parameter array 'RC' is being accessed, the parameter name may
appear in the form "RC(n)", where "n" is an integer between 1 and 16,
inclusive, to select a particular element of the array; additional
characters following the closing parenthesis are ignored.
The second argument is a variable in which the desired value is to be
returned. The type of this argument must be INTEGER in a call to ARGETI
and REAL in a call to ARGETR. If the type of the argument does not match
the type of the internal parameter, the appropriate conversion (using the
intrinsic function INT or REAL) will be done for you.
X and Y coordinates in an area map are represented by integers in the range
from 0 to 'LC', inclusive; the default value of 'LC' is 1,000,000.
The value of 'AT' specifies what sort of arithmetic is to be used by AREAS,
as follows:
- A value less than or equal to 0 allows AREAS to decide what sort of
arithmetic to use. The default value is 0.
- The value 1 implies that real arithmetic is to be used.
- The value 2 implies that double-precision arithmetic is to be used.
- The value 3 implies that multiple-precision integer arithmetic is to be
used and that AREAS should choose the base value to use.
- A value of 4 or greater implies that multiple-precision arithmetic is
to be used and specifies the base value to use. For example, the value
100 would specify the use of base-100 multiple-precision integer
arithmetic.
All calls to AREAS that operate on a particular area map must be done with
the same values of 'LC' and 'AT'. Typically, if the user changes the values,
he/she does it once, at the beginning of his/her program, and then leaves
them unchanged thereafter.
A value given to 'LC' must not be greater than the largest integer on the
machine on which AREAS is running; also, the real value 10.*REAL('LC') must
be exactly representable as a real number on that machine.
Sometimes, if one cannot generate the coordinates of the points defining a
desired set of edge segments to an accuracy of better than one part in
1,000,000, it is desirable to force the use of a smaller value of 'LC';
otherwise, an edge segment that is supposed to join another line segment
at a point other than one of its endpoints may not appear to do so.
Attempting to give 'LC' a value less than 1000 will give it the value
1000.
Using a non-zero value of 'AT' requires some knowledge of the internals
of AREAS and, for the moment, should only be done on recommendation of
the author. Roughly speaking, real arithmetic can be used if the number
'LC'**2 is exactly representable as a real on the machine on which AREAS
is being run and double precision arithmetic can be used if that number
is exactly representable as a double on the machine. Multiple-precision
integer arithmetic is quite a bit slower than real arithmetic and should
only be used as a last resort (if, for example, your compiler will not
handle double precision correctly).
If the user specifies the values of 'LC' and/or 'AT' to be used, the given
values will not be checked for correctness; it is assumed that the user
knows what he/she is doing.
If the value of 'AT' is retrieved, what comes back is either the value
specified by a call to ARSETI, if it was so set, or a value chosen by
AREAS, otherwise.
The default value of the internal parameter 'DB' is zero. If it is set to
a non-zero group identifier G, it forces ARPRAM to produce plots showing
all the edge segments in edge group G, at selected breakpoints. This is
done by calling the routine ARDBPA. To see all groups of edges, set 'DB'
to "-1".
The routine ARDBPA redefines and uses color indices 'DC'+1 through 'DC'+5.
The default value of the internal parameter 'DC' is 100, so ARDBPA will
use color indices 101 through 105; if this would cause a problem, the user
may change 'DC' to force the use of a different set of color indices.
On debug plots, the routine ARDBPA uses arrowheads of length 'AL' and width
2 x 'AW'. Both values are interpreted as fractions of the width of the
plotter frame. Using a value which is less than or equal to zero for either
of these parameters causes the arrowheads to be omitted. The default value
of 'AL' is .008 and the default value of 'AW' is .002.
On debug plots, the routine ARDBPA places area identifiers 'ID' units away
from an edge and uses characters of size 'IS'. Both values are interpreted
as fractions of the width of the plotter frame. Using a value which is less
than or equal to zero for either of these parameters causes the area
identifiers to be omitted. The default value of 'ID' is .004 and the
default value of 'IS' is .001.
If, in preprocessing step 6, as performed by the routine ARPRAM, the
area-identifier information for a particular area defined by a particular
edge group is found to be contradictory, one of the elements of the
internal parameter array 'RC' is used to determine how the contradiction
is to be resolved. See the second-level paragraph
Reconciling Contradictory
Area-Identifier Information, in the "Overview", above.
The parameter array 'RC' is indexed by group identifier. Edge groups with
identifiers greater than 16 are affected by element 16 of 'RC'.
If "RC" appears as the first two characters of the first argument in a
call to ARSETI, all 16 elements in the parameter array are set to the
value specified by the second argument, but if the "RC" is followed by an
integer, enclosed in parentheses, between 1 and 16, inclusive, then the
element of the array 'RC' indexed by that integer is set and other elements
are left unset.
If "RC" appears as the first two characters of the first argument in a
call to ARGETI, the value returned in the second argument is the value of
element 1 of 'RC', but if the "RC" is followed by an integer, enclosed in
parentheses, between 1 and 16, inclusive, then the value returned is the
value of the element of the array 'RC' indexed by that integer.
When an AREAS routine detects an error condition, it calls the routine
SETER, which is the principal routine in the error-handling package for
NCAR Graphics. (There is a programmer document describing SETER and
associated routines; see the Seter
document for complete information about error handling in NCAR Graphics.)
By default, SETER prints a line and STOPs. The line printed will look
something like this:
ERROR 3 IN AREDAM - INITIALIZATION DONE IMPROPERLY
The error number ("3", in the example) may be of use to a consultant (to
determine exactly where the error occurred), but is not otherwise meaningful.
The actual error message consists of the name of the routine in which the
error occurred ("AREDAM", in the example), a blank, a minus sign, another
blank, and, lastly, a short description of the error.
All errors are "recoverable" in the sense that, if the user program puts
SETER into "recovery" mode, control will be returned to the caller of the
AREAS routine in which the error occurred. In some cases, it is then possible
to take remedial action to get around whatever problem has occurred; in any
case, the error flag can be cleared and execution of the user's program can
continue. (The example "arex02" may be helpful; it
shows how to recover, albeit somewhat clumsily, from area-map array overflows
in a Fortran 77 context.)
When SETER is in recovery mode (and, occasionally, even when it is not),
error messages may have a somewhat more complicated form, like this:
ARSCAM/ARPRAM - AREA-MAP ARRAY OVERFLOW
What this particular error message says is that ARSCAM called ARPRAM, which
detected an error condition (area-map array overflow) and called SETER. Upon
getting control back from ARPRAM, ARSCAM detected the fact that ARPRAM had
logged an error. It augmented the error message by prepending its own name,
followed by a slash, and then passed control back to the user. Of course,
there can be more than two such levels of routine calls indicated in the
error message: in a few cases, seven or eight routine names may be listed,
each separated from the next by a slash.
The various error conditions in AREAS are described in the list below. Each
bulleted item includes an error message and a thumb-nail description of the
error. The items in the list are arranged in alphabetical order. If you get
an error message with one or more prefixed subroutine names, as described
above, omit them and look up the result in this list. Note that, since AREAS
routines sometimes call other routines, elsewhere in NCAR Graphics, that can
detect error conditions and call SETER, the error message you get by calling
an AREAS routine may not be listed here, but in the programmer document for
some other package.
- ARDBDA - UNCLEARED PRIOR ERROR
- ARDBDA is an internal routine called by ARDBPA; it draws an arrow on a
debug plot. This error message indicates that, at the time ARDBDA was called,
there was an unrecovered outstanding error. In this case, ARDBDA cannot
continue; it forces the error message for the outstanding error to be printed
and then substitutes this one for it.
- ARDBPA - BAD POINTERS IN AREA MAP
- ARDBPA has found pointers in the area map that either point outside
the area-map array or point to locations inside the array which cannot be
correct. This very likely means that the user has somehow written over
the area-map array.
- ARDBPA - ERROR EXIT FROM GQPLCI
- The GKS routine GQPLCI, which is called to get the current value of the
polyline color index, has returned a non-zero error code.
- ARDBPA - ERROR EXIT FROM GQTXCI
- The GKS routine GQTXCI, which is called to get the current value of the
text color index, has returned a non-zero error code.
- ARDBPA - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARDBPA did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- ARDBPA - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARDBPA was called, there
was an unrecovered outstanding error. In this case, ARDBPA cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARDRLN - ALGORITHM FAILURE
- An "impossible" situation has arisen. The line that was to be drawn by
ARDRLN will be incomplete. Real recovery is not possible, but execution of
the user's program can be made to continue.
- ARDRLN - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARDRLN did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- The arrays in which information about group identifiers and area
identifiers are to be passed to the line-processing routine are not long
enough. Normally, it is sufficient to use arrays of length "n", where "n"
is the number of different group identifiers used for the edges in the area
map.
- ARDRLN - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARDRLN was called, there
was an unrecovered outstanding error. In this case, ARDRLN cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- AREDAM - AREA-MAP ARRAY OVERFLOW
- The area map array is too small. Recovery may be effected by moving the
area map to a new array (using a call to ARMVAM) and then repeating the call
that resulted in the error, using the new array.
- AREDAM - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to AREDAM did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- AREDAM - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time AREDAM was called, there
was an unrecovered outstanding error. In this case, AREDAM cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARGETI - PARAMETER NAME NOT KNOWN - X
- The first argument in a call to ARGETI does not match the name of any of
the internal parameters of AREAS. In the error message, "X" represents the
value of the offending argument.
- ARGETI - PARAMETER NAME TOO SHORT - X
- This error results from calling ARGETI with a 1-character first argument,
which is too short to contain the name of any internal parameter of AREAS. In
the error message, "X" represents the value of the offending argument.
- ARGETI - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARGETI was called, there
was an unrecovered outstanding error. In this case, ARGETI cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARGETI - 'RC' INDEX IS OUT OF RANGE
- This error message indicates that the name of the parameter is given in
the form "RC(n)", and the value of the integer "n" is either less than 1 or
bigger than 16.
- ARGETR - PARAMETER NAME NOT KNOWN - X
- The first argument in a call to ARGETR does not match the name of any of
the internal parameters of AREAS. In the error message, "X" represents the
value of the offending argument.
- ARGETR - PARAMETER NAME TOO SHORT - X
- This error results from calling ARGETR with a 1-character first argument,
which is too short to contain the name of any internal parameter of AREAS.
In the error message, "X" represents the value of the offending argument.
- ARGETR - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARGETR was called, there
was an unrecovered outstanding error. In this case, ARGETR cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARGETR - 'RC' INDEX IS OUT OF RANGE
- This error message indicates that the name of the parameter is given in
the form "RC(n)", and the value of the integer "n" is either less than 1 or
bigger than 16.
- ARGTAI - ALGORITHM FAILURE
- An "impossible" situation has arisen. The information returned by the
call to ARGTAI will be incomplete/erroneous. Real recovery is not possible,
but execution of the user's program can be made to continue.
- ARGTAI - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARGTAI did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- The arrays in which ARGTAI is to return information about area
identifiers and group identifiers are either too small or the value of the
argument MAI does not correctly specify the lengths of these arrays.
Normally, it is sufficient to use arrays of length "n", where "n" is the
number of different group identifiers used for the edges in the area map.
- ARGTAI - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARGTAI was called, there
was an unrecovered outstanding error. In this case, ARGTAI cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARINAM - AREA-MAP ARRAY IS TOO SMALL
- The area map array is too small. In this case, "too small" means "less
than 28 words". An area map array has to be much larger than that.
- ARINAM - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARINAM was called, there
was an unrecovered outstanding error. In this case, ARINAM cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARINIT - VALUE OF 'LC' IS TOO LARGE
- ARINIT is an internal routine that is called by other routines of AREAS
to compute certain needed quantities. The value of the internal parameter
'LC' is too large for the hardware on which AREAS is being run. This is
probably the result of a user's ill-advised specification of the value of
this parameter.
- ARMPIA - MULTIPLE-PRECISION QUANTITY IS TOO BIG
- ARMPIA is an internal routine that does multiple-precision arithmetic.
Such arithmetic is being used and an intermediate result has been generated
which is too large to be represented correctly. This is almost certainly the
result of AREAS having been installed incorrectly.
- ARMVAM - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARMVAM did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- ARMVAM - NEW AREA-MAP ARRAY IS TOO SMALL
- The area map array to which an area map is to be moved, as specified by
the values of the second and third arguments in the call to ARMVAM, is too
small to hold the area map.
- ARMVAM - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARMVAM was called, there
was an unrecovered outstanding error. In this case, ARMVAM cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARPRAM - ALGORITHM FAILURE
- An "impossible" situation has arisen. Preprocessing of the area map has
been abandoned and further use of the area map will probably result in other
errors. Real recovery is not possible, but execution of the user's program
can be made to continue.
- ARPRAM - AREA-MAP ARRAY OVERFLOW
- The area map array is too small. Recovery may be effected by moving the
area map to a new array (using a call to ARMVAM) and then repeating the call
that resulted in the error, using the new array.
- ARPRAM - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARPRAM did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- ARPRAM - NO EDGES IN AREA MAP
- The area map appears to have the correct form, but no edges have ever
been put into it.
- ARPRAM - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARPRAM was called, there
was an unrecovered outstanding error. In this case, ARPRAM cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARSCAM - ALGORITHM FAILURE
- An "impossible" situation has arisen. Scanning of areas defined by the
area map is incomplete. Real recovery is not possible, but execution of the
user's program can be made to continue.
- ARSCAM - AREA-MAP ARRAY OVERFLOW
- The area map array is too small. Recovery may be effected by moving the
area map to a new array (using a call to ARMVAM) and then repeating the call
that resulted in the error, using the new array.
- ARSCAM - INITIALIZATION DONE IMPROPERLY
- A simple check indicated that the area map array passed to ARSCAM did
not appear to contain an area map. This may mean simply that the name of
the area map array was misspelled in the call or it may indicate something
more serious.
- The arrays in which information about group identifiers and area
identifiers are to be passed to the area-processing routine are not long
enough. Normally, it is sufficient to use arrays of length "n", where "n"
is the number of different group identifiers used for the edges in the area
map.
- The arrays in which X and Y coordinates are to be passed to the
area-processing routine are not long enough. Some sub-area defined by the
area map is complicated enough to require more coordinates than those arrays
allow for.
- ARSCAM - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARSCAM was called, there
was an unrecovered outstanding error. In this case, ARSCAM cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARSETI - PARAMETER NAME NOT KNOWN - X
- The first argument in a call to ARSETI does not match the name of any of
the internal parameters of AREAS. In the error message, "X" represents the
value of the offending argument.
- ARSETI - PARAMETER NAME TOO SHORT - X
- This error results from calling ARSETI with a 1-character first argument,
which is too short to contain the name of any internal parameter of AREAS.
In the error message, "X" represents the value of the offending argument.
- ARSETI - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARSETI was called, there
was an unrecovered outstanding error. In this case, ARSETI cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARSETI - 'RC' INDEX IS OUT OF RANGE
- This error message indicates that the name of the parameter is given in
the form "RC(n)", and the value of the integer "n" is either less than 1 or
bigger than 16.
- ARSETR - PARAMETER NAME NOT KNOWN - X
- The first argument in a call to ARSETR does not match the name of any
of the internal parameters of AREAS. In the error message, "X" represents
the value of the offending argument.
- ARSETR - PARAMETER NAME TOO SHORT - X
- This error results from calling ARSETR with a 1-character first argument,
which is too short to contain the name of any internal parameter of AREAS.
In the error message, "X" represents the value of the offending argument.
- ARSETR - UNCLEARED PRIOR ERROR
- This error message indicates that, at the time ARSETR was called, there
was an unrecovered outstanding error. In this case, ARSETR cannot continue;
it forces the error message for the outstanding error to be printed and then
substitutes this one for it.
- ARSETR - 'RC' INDEX IS OUT OF RANGE
- This error message indicates that the name of the parameter is given in
the form "RC(n)", and the value of the integer "n" is either less than 1 or
bigger than 16.
This section presents details that most users will not care about, but that
may be useful to a few.
The phrase "the representation of an area map", used above to refer to the
contents of an area map array, was carefully chosen to reflect the fact
that, since only integers can be stored in the area map array, one cannot
truly deal with an arbitrary area map in Euclidean space; one can only
approximate that area map in a discrete, non-Euclidean space. This has
been responsible for much of the difficulty of writing AREAS and making
it work properly.
In particular, since X and Y coordinates are represented by integers in a
limited range, an area map array created by AREAS cannot represent all
possible area maps; it can only represent those constructed from edge
segments that lie in a square bounded by the lines X = 0, X = 'LC', Y = 0,
and Y ='LC'. Even within that square, only those area maps can be
represented whose member edge segments join points whose X and Y
coordinates are expressible as integers.
The elements of an area map array IAM, of length LAM, are as follows:
| Element | Contents |
| 1 | The length of the area map array (= LAM). |
| 2 | The greatest value of ABS(X(P)-X(Q)), where P and Q are the
endpoints of an edge segment in the area map, X(P) is the X
coordinate of P, and X(Q) is the X coordinate of Q. |
| 3 | The index of the last "node" worked with (preserved from call to
call for reasons of efficiency). |
| 4 | The area map state. It is set to zero initially and again whenever
more edge segments are added to the area map; it is set to one by
the routine ARPRAM, which is called to "preprocess" the area map. |
| 5 | The index of the last element used at the beginning of the area map
array (initially set to 27). |
| 6 | The index of the last element used at the end of the area map array
(initially set to LAM). |
| 7 | The number of edge groups that currently occur in the area map. |
| 8 to 17 | A dummy node in the area map, anchoring the beginning of the
linked list of nodes. |
| 18 to 27 | A dummy node in the area map, anchoring the end of the linked
list of nodes. |
| 28 to IAM(5) | Nodes added to the area map by calls to the routine AREDAM,
each representing a point in the plane. |
| IAM(5)+1 to IAM(6)-1 | Unused. |
| IAM(6) to LAM-1 | Values of group and area identifiers. |
| LAM | The length of the area map array (= LAM). This element is set to
allow a rudimentary test for user error (if he/she calls one of the
AREAS routines with an area map array that has not been initialized). |
Note that space at the beginning of the area map array is used to store
"nodes" and that space at the end of the area map array is used to store
group and area identifiers.
Each "node" in an area map consists of ten elements and represents a single
point in the plane. The ten elements are as follows:
| Element | Contents |
| 1 | A "flag cell" for the node, used in various ways by the routines
ARPRAM and ARSCAM during processing of the area map. |
| 2 | The X coordinate of the point defined by the node, in the range
from 0 to 'LC'. |
| 3 | The Y coordinate of the point defined by the node, in the range
from 0 to 'LC'. |
| 4 | A pointer to the next node (in "drawing" order). |
| 5 | A pointer to the previous node (in "drawing" order). |
| 6 | A pointer to the next node (in "coordinate" order). |
| 7 | A pointer to the previous node (in "coordinate" order). |
| 8 | If non-zero, a pointer to the group identifier for an edge segment. |
| 9 | If greater than zero, a pointer to the left area identifier for an edge
segment. Otherwise, the area identifier itself. |
| 10 | If greater than zero, a pointer to the right area identifier for an edge
segment. Otherwise, the area identifier itself. |
If element 8 of a node is non-zero, it implies that the node defines the
endpoint of an edge segment in the area map (the node pointed to by element
5 defines the other endpoint of the edge segment). If element 8 is zero,
then the line segment joining the point defined by the node to the point
defined by the node that element 5 points to is not an edge segment in the
area map.
On a Unix system on which NCAR Graphics has been installed, the command
"ncargex" may be used to acquire the code for and run the following examples
illustrating various capabilities of AREAS:
- The example named "tareas" produces a single frame demonstrating minimal
functioning of AREAS.
- The example named "arex01" produces a set of frames showing, in detail,
what ARPRAM does to an area map.
(frame 29)
- The example named "arex02" illustrates the process of recovering from
overflow errors.
(frame 1)
- The example named "arex03" produces two frames showing the effects of
using different values in the parameter array 'RC' (each element of which
determines how contradictory area-identifier information for a particular
group is to be reconciled). Shown are five rows of decagons, with ten
decagons in each row (five on frame 1 and five on frame 2). Each row of
decagons is associated with a particular element of 'RC'. Within each
decagon, in small characters, are written the ten area identifiers
associated with the interior of the decagon by its ten edge segments.
The sizes of the characters used to write these area identifiers reflects
the order in which they were delivered to AREDAM: The area identifier
delivered to AREDAM first is written in the smallest characters and the
one delivered to AREDAM last is written in the largest characters. The
set of area identifiers used is the same for all the decagons in a
particular vertical column. In the middle of each decagon, in large
characters, is written the final area identifier chosen for the decagon
by using the reconciliation method implied by the row that the decagon
is in.
(frame 1)
(frame 29)
(frame 1)
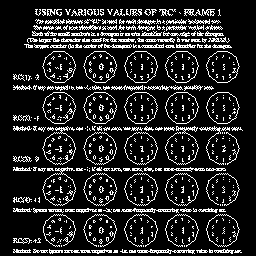(frame 1)